
https://www.acmicpc.net/problem/14500
14500번: 테트로미노
폴리오미노란 크기가 1×1인 정사각형을 여러 개 이어서 붙인 도형이며, 다음과 같은 조건을 만족해야 한다. 정사각형은 서로 겹치면 안 된다. 도형은 모두 연결되어 있어야 한다. 정사각형의 변
www.acmicpc.net
문제
폴리오미노란 크기가 1×1인 정사각형을 여러 개 이어서 붙인 도형이며, 다음과 같은 조건을 만족해야 한다.
- 정사각형은 서로 겹치면 안 된다.
- 도형은 모두 연결되어 있어야 한다.
- 정사각형의 변끼리 연결되어 있어야 한다. 즉, 꼭짓점과 꼭짓점만 맞닿아 있으면 안 된다.
정사각형 4개를 이어 붙인 폴리오미노는 테트로미노라고 하며, 다음과 같은 5가지가 있다.
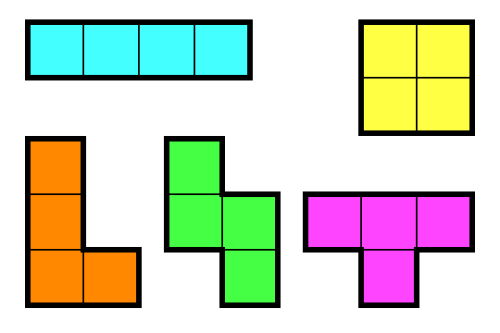
아름이는 크기가 N×M인 종이 위에 테트로미노 하나를 놓으려고 한다. 종이는 1×1 크기의 칸으로 나누어져 있으며, 각각의 칸에는 정수가 하나 쓰여 있다.
테트로미노 하나를 적절히 놓아서 테트로미노가 놓인 칸에 쓰여 있는 수들의 합을 최대로 하는 프로그램을 작성하시오.
테트로미노는 반드시 한 정사각형이 정확히 하나의 칸을 포함하도록 놓아야 하며, 회전이나 대칭을 시켜도 된다.
입력
첫째 줄에 종이의 세로 크기 N과 가로 크기 M이 주어진다. (4 ≤ N, M ≤ 500)
둘째 줄부터 N개의 줄에 종이에 쓰여 있는 수가 주어진다. i번째 줄의 j번째 수는 위에서부터 i번째 칸, 왼쪽에서부터 j번째 칸에 쓰여 있는 수이다. 입력으로 주어지는 수는 1,000을 넘지 않는 자연수이다.
출력
첫째 줄에 테트로미노가 놓인 칸에 쓰인 수들의 합의 최댓값을 출력한다.
(첫번째 풀이)
알고리즘을 오래 쉬다보니, 단순하게 완전탐색(Brute Force)으로 풀이하는것이 가장 먼저 떠올랐다.
(1) 단순무식하게 각각의 테트로미노로 만들 수 있는 모든 경우(19가지)를 미리 등록한다.

(2) NxM의 arr를 전부 순회하며 19개의 블록을 놓아본다. (판의 범위를 초과하는 경우 패스)
(3) 블록을 놓았을 때 구해지는 sum값의 최댓값인 maxsum을 구한다.
--> 19개 상태에 대해 등록을 해두고 문제를 풀다보니 단순히 N * M * 19 번 반복문을 수행하는 식으로 풀이는 간단해졌다.
(but, 19개를 모두 등록해두는게 매우 번거롭고 비효율적이라는 문제가... )
import sys
# 5개 테트로미노 # 총 19개 가능성
di = [[0, 0, 0, 0], [0, 1, 2, 3],
[0, 0, 1, 1],
[0, 1, 2, 2], [0, 1, 0, 0], [0, 0, 1, 2], [1, 1, 1, 0],
[2, 2, 1, 0], [0, 1, 1, 1], [0, 0, 1, 2], [0, 0, 0, 1],
[0, 1, 1, 2], [1, 1, 0, 0],
[0, 1, 1, 2], [0, 0, 1, 1],
[0, 0, 0, 1], [1, 0, 1, 2], [0, 1, 1, 1] ,[0, 1, 2, 1]]
dj = [[0, 1, 2, 3], [0, 0, 0, 0],
[0, 1, 0, 1],
[0, 0, 0, 1], [0, 0, 1, 2], [0, 1, 1, 1], [0, 1, 2, 2],
[0, 1, 1, 1], [0, 0, 1, 2], [0, 1, 0, 0], [0, 1, 2, 2],
[0, 0, 1, 1], [0, 1, 1, 2],
[1, 1, 0, 0], [0, 1, 1, 2],
[0, 1, 2, 1], [0, 1, 1, 1], [1, 0, 1, 2] ,[0, 0, 0, 1]]
def blckSum(i, j):
global maxsum
for a in range(19):
sum = 0
for n in range(4):
ni, nj = i + di[a][n], j + dj[a][n]
if ni >= 0 and ni < N and nj >= 0 and nj < M:
sum += arr[ni][nj]
else:
sum = 0
break
maxsum = max(sum, maxsum)
### main
N, M = map(int, sys.stdin.readline().split())
arr = []
maxsum = -1
for _ in range(N):
arr.append(list(map(int, sys.stdin.readline().split())))
for i in range(N):
for j in range(M):
blckSum(i, j)
print(maxsum)(두번째 풀이)
문제에 "도형은 모두 연결되어 있어야 한다." 라는 조건이 있다.
즉, dfs로 블록 4개를 선택하면 된다. 그리고 'ㅏ' 모양의 블록은 별도로 구해줘야한다.
나는 combination(조합)을 통해 'ㅏ' 블록을 선택했다.

--> 위 그림과 같이 현재 위치 선택 & 상, 하, 좌, 우 4개 위치에서 3개의 블록을 선택 (4C3)
하지만,, 이 풀이에서 시간초과의 늪에 빠져버렸다..
예전에 자바로 동일하게 dfs풀이를 했을 때는 문제가 없었는데, Python언어의 속도문제인걸로 보인다.
의외로 간단하게 이 문제는 제출언어를 python3 -> PyPy3 으로 변경하며 해결되었다.
++ 추가로, 아래와 같이 중복되는 선택 케이스를 없에 시간을 줄이기 위해서
dfs에서 4방향으로 탐색하지않고, 3방향으로만 탐색하였다. ('위' 방향으로는 탐색X)


import sys
di = [0, 1, 0, -1]
dj = [1, 0, -1, 0]
def dfs(i, j, sum, cnt):
global maxsum
if cnt == 4:
maxsum = max(maxsum, sum)
return
for n in range(3):
ni, nj = i + di[n], j + dj[n]
if(ni >=0 and ni < N and nj >=0 and nj < M and not vi[ni][nj]):
vi[ni][nj] = True
dfs(ni, nj, sum+arr[ni][nj], cnt+1)
vi[ni][nj] = False
def comb(i, j, sum, sta, cnt):
global maxsum
if cnt == 4:
maxsum = max(maxsum, sum)
return
for n in range(sta, 4):
ni, nj = i + di[n], j + dj[n]
if(ni >=0 and ni < N and nj >=0 and nj < M):
comb(i, j, sum + arr[ni][nj], n+1, cnt+1)
## main
N, M = map(int, sys.stdin.readline().split())
maxsum = 0
arr = []
for _ in range(N):
arr.append(list(map(int, sys.stdin.readline().split())))
vi = [[False for _ in range(M)] for _ in range(N)]
for i in range(N):
for j in range(M):
vi[i][j] = True
dfs(i, j, arr[i][j], 1)
vi[i][j] = False
comb(i, j, arr[i][j], 0, 1)
print(maxsum)'Algorithm > 문제풀이' 카테고리의 다른 글
| [Python][백준] 16968_차량 번호판 1 (0) | 2021.06.06 |
|---|---|
| [Python][백준] 1107_리모컨 (0) | 2021.06.06 |
| [Python][백준] 1182_부분수열의 합 (0) | 2021.05.21 |
| [Python][백준] 1759_암호 만들기 (0) | 2021.05.17 |
| [Python][백준] 1476_날짜 계산 (0) | 2021.05.17 |