
https://www.acmicpc.net/problem/11062
11062번: 카드 게임
근우와 명우는 재미있는 카드 게임을 하고 있다. N개의 카드가 일렬로 놓여 있다. 각 카드에는 점수가 적혀있다. 근우부터 시작하여 번갈아가면서 턴이 진행되는데 한 턴에는 가장 왼쪽에 있는
www.acmicpc.net
문제
근우와 명우는 재미있는 카드 게임을 하고 있다. N개의 카드가 일렬로 놓여 있다. 각 카드에는 점수가 적혀있다. 근우부터 시작하여 번갈아가면서 턴이 진행되는데 한 턴에는 가장 왼쪽에 있는 카드나 가장 오른쪽에 있는 카드를 가져갈 수 있다. 카드가 더 이상 남아있지 않을 때까지 턴은 반복된다. 게임의 점수는 자신이 가져간 카드에 적힌 수의 합이다.
근우와 명우는 서로 자신의 점수를 가장 높이기 위해 최선의 전략으로 게임에 임한다. 놓여있는 카드의 개수 N과 카드가 놓여있는 상태가 주어졌을 때 근우가 얻는 점수를 구하는 프로그램을 작성하시오.
예를 들어 카드가 [4, 3, 1, 2]로 놓여있다고 하자. 근우는 처음에 4가 적힌 카드를 가져가고, 명우는 3이 적힌 카드를 가져간다. 그리고 근우는 2가 적힌 카드를 가져가고, 명우는 마지막으로 1이 적힌 카드를 가져간다. 이때 근우와 명우는 최선의 전략으로 임했으며, 근우가 얻는 점수는 6이다.
입력
입력의 첫 줄에는 테스트케이스의 수 T가 주어진다.
각 테스트케이스 마다 첫 줄에는 카드의 개수 N(1 ≤ N ≤ 1,000)이 주어진다. 두 번째 줄에는 N개의 자연수가 공백으로 구분되어 주어지는데, i번째로 주어지는 수는 왼쪽에서 i번째에 놓인 카드에 적힌 수를 의미한다. 카드에 적혀있는 수는 1이상 10,000이하다.
출력
각 테스트케이스마다 근우와 명우가 최선의 전략으로 임할 때 근우가 얻게되는 점수를 줄로 구분하여 출력한다.
풀이보다는 아이디어 찾는데 더 많은 시간이 소요되었던 문제이다.
내가 왼쪽/오른쪽을 선택했을 때 추후에 상대방이 선택할 카드의 합이 최소가 되어야 하기 때문에
맨 왼쪽/오른쪽 카드의 수만 비교해서는 최선의 선택이 되지 않는다.
그렇기 때문에, 그리디 접근은 X, 다이나믹 프로그래밍(DP)으로 접근했다.
[고려사항]
- 근우의 차례인지 명우의 차례인지에 따라 DP를 구하는 식이 다르다.
- 2차원 배열을 사용하는 아이디어가 필요하다.
[풀이]
1. DP의 점화식을 만들어 내기 위해 가장 작은 단위로 쪼개보자.
: 선우와 명우가 카드를 선택하다가 남은 카드의 상태를 좌표로 나타내면 다음과 같다.

이를 이용하여 dp[i][j] = i~j 의 카드가 있을 때 근우가 선택할 수 있는 최대 합 이라는 식을 만들 수 있다.
2. 근우 / 명우차례일 때 식을 나누자.
: N이 홀수이면 남은 카드의 수가 홀수일 때가 근우차례, N이 짝수이면 카드의 수가 짝수일 때가 근우차례이다.
turn = True if N % 2 == 1 else False # True일 때 근우차례근우차례: i~j 카드가 있을 때, 선택할 카드(i or j) + 다음에 선택할 카드의 합이 최대가 되도록 선택한다.
명우차례: i~j 카드가 있을 때, 명우의 선택(i or j) 후 남은 카드들로 근우가 선택할 카드의 합이 최소가 되도록 선택한다.
3. 점화식 구하기
(카드가 1개 남았을 때)
근우의 차례가 아니면, 카드선택을 하지 않으므로 dp[0][0], dp[1][1].. 에 들어갈 값은 0이다.

if size == 0:
dp[i][i+size] = arr[i] if turn else 0단, 위 예시에서는 전체 카드수 N이 짝수이므로 카드가 1개일 때는 명우차례이다.
(카드가 2개 남았을 때)
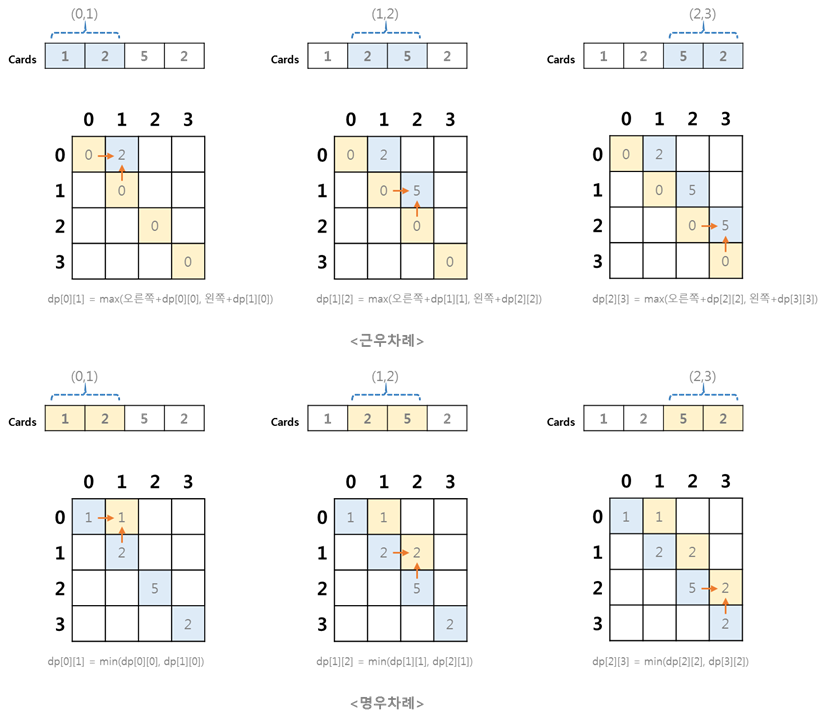
단, 위 예시에서는 전체 카드수 N이 짝수이므로 카드가 2개일 때는 근우차례이다.
(점화식)
# if 근우차례
dp[i][i+size] = max(dp[i+1][i+size] + arr[i], dp[i][i+size-1] + arr[i+size])
# if 명우차례
dp[i][i+size] = min(dp[i+1][i+size], dp[i][i+size-1])
[전체코드]
import sys, heapq
T = int(sys.stdin.readline())
for t in range(T):
N = int(sys.stdin.readline())
arr = list(map(int, sys.stdin.readline().strip().split()))
dp = [[0 for _ in range(N)] for _ in range(N)]
turn = True if N % 2 == 1 else False # True일 때 근우차례
for size in range(N):
for i in range(N - size):
if size == 0:
dp[i][i+size] = arr[i] if turn else 0
elif turn: #근우차례
dp[i][i+size] = max(dp[i+1][i+size] + arr[i], dp[i][i+size-1] + arr[i+size])
else: #명우차례
dp[i][i+size] = min(dp[i+1][i+size], dp[i][i+size-1])
turn = not turn #차례바꿈
print(dp[0][N-1])
이걸 계산하면서 카드를 선택했다니.. 근우와 명우는 엄청나게 똑똑한 아이들이었다.
'Algorithm > 문제풀이' 카테고리의 다른 글
| [Python][백준] 11657_타임머신 (0) | 2021.07.15 |
|---|---|
| [Python][백준] 2211_네트워크 복구 (0) | 2021.07.15 |
| [Python][백준] 1916_최소비용 구하기 (0) | 2021.07.09 |
| [Python][백준] 4485_녹색 옷 입은 애가 젤다지? (0) | 2021.07.09 |
| [Python][백준] 3055_탈출 (0) | 2021.07.06 |