2019 KAKAO BLIND RECRUITMENT
https://programmers.co.kr/learn/courses/30/lessons/42892
코딩테스트 연습 - 길 찾기 게임
[[5,3],[11,5],[13,3],[3,5],[6,1],[1,3],[8,6],[7,2],[2,2]] [[7,4,6,9,1,8,5,2,3],[9,6,5,8,1,4,3,2,7]]
programmers.co.kr
문제 설명
길 찾기 게임
전무로 승진한 라이언은 기분이 너무 좋아 프렌즈를 이끌고 특별 휴가를 가기로 했다.
내친김에 여행 계획까지 구상하던 라이언은 재미있는 게임을 생각해냈고 역시 전무로 승진할만한 인재라고 스스로에게 감탄했다.
라이언이 구상한(그리고 아마도 라이언만 즐거울만한) 게임은, 카카오 프렌즈를 두 팀으로 나누고, 각 팀이 같은 곳을 다른 순서로 방문하도록 해서 먼저 순회를 마친 팀이 승리하는 것이다.
그냥 지도를 주고 게임을 시작하면 재미가 덜해지므로, 라이언은 방문할 곳의 2차원 좌표 값을 구하고 각 장소를 이진트리의 노드가 되도록 구성한 후, 순회 방법을 힌트로 주어 각 팀이 스스로 경로를 찾도록 할 계획이다.
라이언은 아래와 같은 특별한 규칙으로 트리 노드들을 구성한다.
- 트리를 구성하는 모든 노드의 x, y 좌표 값은 정수이다.
- 모든 노드는 서로 다른 x값을 가진다.
- 같은 레벨(level)에 있는 노드는 같은 y 좌표를 가진다.
- 자식 노드의 y 값은 항상 부모 노드보다 작다.
- 임의의 노드 V의 왼쪽 서브 트리(left subtree)에 있는 모든 노드의 x값은 V의 x값보다 작다.
- 임의의 노드 V의 오른쪽 서브 트리(right subtree)에 있는 모든 노드의 x값은 V의 x값보다 크다.
아래 예시를 확인해보자.
라이언의 규칙에 맞게 이진트리의 노드만 좌표 평면에 그리면 다음과 같다. (이진트리의 각 노드에는 1부터 N까지 순서대로 번호가 붙어있다.)
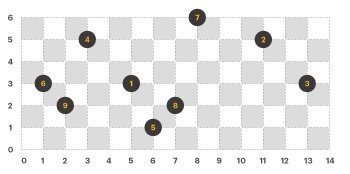
이제, 노드를 잇는 간선(edge)을 모두 그리면 아래와 같은 모양이 된다.
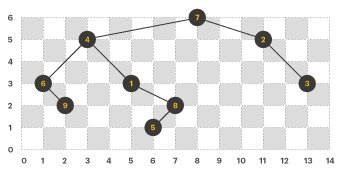
위 이진트리에서 전위 순회(preorder), 후위 순회(postorder)를 한 결과는 다음과 같고, 이것은 각 팀이 방문해야 할 순서를 의미한다.
- 전위 순회 : 7, 4, 6, 9, 1, 8, 5, 2, 3
- 후위 순회 : 9, 6, 5, 8, 1, 4, 3, 2, 7
다행히 두 팀 모두 머리를 모아 분석한 끝에 라이언의 의도를 간신히 알아차렸다.
그러나 여전히 문제는 남아있다. 노드의 수가 예시처럼 적다면 쉽게 해결할 수 있겠지만, 예상대로 라이언은 그렇게 할 생각이 전혀 없었다.
이제 당신이 나설 때가 되었다.
곤경에 빠진 카카오 프렌즈를 위해 이진트리를 구성하는 노드들의 좌표가 담긴 배열 nodeinfo가 매개변수로 주어질 때,
노드들로 구성된 이진트리를 전위 순회, 후위 순회한 결과를 2차원 배열에 순서대로 담아 return 하도록 solution 함수를 완성하자.
제한사항
nodeinfo는 이진트리를 구성하는 각 노드의 좌표가 1번 노드부터 순서대로 들어있는 2차원 배열이다.- nodeinfo의 길이는 1 이상 10,000 이하이다.
- nodeinfo[i] 는 i + 1번 노드의 좌표이며, [x축 좌표, y축 좌표] 순으로 들어있다.
- 모든 노드의 좌표 값은 0 이상 100,000 이하인 정수이다.
- 트리의 깊이가 1,000 이하인 경우만 입력으로 주어진다.
- 모든 노드의 좌표는 문제에 주어진 규칙을 따르며, 잘못된 노드 위치가 주어지는 경우는 없다.
풀이 방법이 쉽게 떠오르지 않아 결국에는 다른 사람의 풀이를 참고하였다. 문제의 핵심은 재귀를 통해 어떻게 트리를 만들어내느냐이다.
[재귀로 트리 만들기]
참고한 풀이에서는 Tree라는 class를 만들어 주었는데, 나는 대신 (leftSubTree, rightSubTree, nodeIndex) 값을 return 해주는 재귀함수를 통해 풀이하였다.
1. 주어진 nodeinfo에 index 값을 추가하고, y의 역순으로 정렬해준다.
-> y 레벨을 통해 parent, child가 판단됨
nodes = [(idx+1, x, y) for idx, (x, y) in enumerate(nodeinfo)]
nodes = sorted(nodes, key=lambda x: x[2] * -1)
2. y 레벨이 제일 큰 parent node부터 시작하여 재귀로 leftSubTree와 rightSubTree를 구해줌
-> leftSubTree의 경우 parent node보다 x값이 작고, rightSubTree의 경우 parent node보다 x값이 크다.
left, right의 서브트리를 어떻게 구할것인가에 대한 고민이 있었는데, filter를 통해 parent의 x와 크기를 비교하여 구할 수 있다는 것이 포인트였다.
parent = nodes[0]
leftNodes = list(filter(lambda x: x[1] < parent[1], nodes))
rightNodes = list(filter(lambda x: x[1] > parent[1], nodes))
left = getSubTree(leftNodes) if leftNodes else False
right = getSubTree(rightNodes) if rightNodes else False
return (left, right, parent[0])
[전위 순회, 후위 순회]
다음의 순서대로, 재귀를 통해 구현된다. 이건 그냥 외워주는게 좋을 것 같다.
전위 순회 (Preorder): parent -> preorder(left) -> preorder(right) 순
후위 순회 (Postorder): postorder(left) -> postorder(right) -> parent 순
* 주의: 이대로 제출시에 2개 케이스에서 런타임 에러가 발생하는데, 이는 python의 default recursive depth 를 초과했기 때문이다.
sys.setrecursionlimit(10**5) 로 limit를 증가시키면 해결된다.
import sys
sys.setrecursionlimit(10**5)
def getSubTree(nodes):
parent = nodes[0]
leftNodes = list(filter(lambda x: x[1] < parent[1], nodes))
rightNodes = list(filter(lambda x: x[1] > parent[1], nodes))
left = getSubTree(leftNodes) if leftNodes else False
right = getSubTree(rightNodes) if rightNodes else False
return (left, right, parent[0])
# parent -> left -> right
def preOrder(tree, pre):
pre.append(tree[2])
preOrder(tree[0], pre) if tree[0] else None
preOrder(tree[1], pre) if tree[1] else None
return pre
# left -> right -> parent
def postOrder(tree, post):
postOrder(tree[0], post) if tree[0] else None
postOrder(tree[1], post) if tree[1] else None
post.append(tree[2])
return post
def solution(nodeinfo):
# left, right sub tree를 recursive를 통해 구해줌
nodes = [(idx+1, x, y) for idx, (x, y) in enumerate(nodeinfo)]
nodes = sorted(nodes, key=lambda x: x[2] * -1)
tree = getSubTree(nodes) # (leftTree, rightTree)
pre, post = [], []
pre = preOrder(tree, pre)
post = postOrder(tree, post)
return [pre, post]
'Algorithm > 문제풀이' 카테고리의 다른 글
| [Python][백준] 2716_원숭이 매달기 (0) | 2022.03.02 |
|---|---|
| [Python][백준] 11725_트리의 부모 찾기 (0) | 2022.02.28 |
| [Python][백준] 9205_맥주 마시면서 걸어가기 (0) | 2022.02.22 |
| [Python][백준] 1922_네트워크 연결 (0) | 2022.02.22 |
| [Python][백준] 2644_촌수계산 (0) | 2022.02.22 |